동적 계획법

특정 법위까지의 값을 구하기 위해서 그것과 다른 범위까지의 값을 이용하여 효율적으로 값을 구하는 알고리즘을 동적 계획법, DP라고 한다.
쉽게 말해서 이전 계산까지의 결과를 활용하여 문제를 푸는 것이다. 그렇기 때문에 동적 계획법은 특정 답을 구하기 위해 같은 계산을 여러번 해야하는 데, 이는 최적 부분 구조(Optimal Substructure)의 문제를 푸는데 greedy algorithm을 사용하는 것 보다 큰 효과를 발휘한다.
접근
동적 계획법의 접근 방식은 원래의 문제를 작은 부분 문제들의 연속된 절차로 바꾸는 과정에서 분할 정복 알고리즘과 유사하다.
즉, 지금까지 쓴 글을 종합해보면 동적 계획법이란
최적 부분 구조를 지닌 중복된 하위 문제를 분할 정복으로 풀이하는 문제 해결 패러다임이라고 할 수 있다.
동적 계획법의 대표적인 예로는 피보나치 수열이 있다.
피보나치 수열(DP ver.)
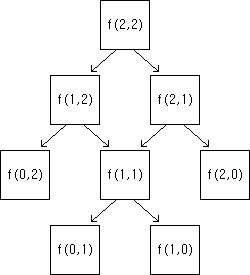
다음 f함수는
- f(a,b) = f(a-1,b) + f(a,b-1) (a,b >= 1 )
-
f(0,0) = 1, 임의의 자연수 n에 대해 f(n,0) = f(0,n) = 1
인 함수이다. 해당 피보나치 함수를 실행 시키면 중복되는 답의 경우인 f(1,1)의 연산이 기존 2번 연산에서 DP를 적용시키면 1번만 함으로써 불필요한 연산을 줄일 수 있다는 장점이 있다. 물론 연산하나가 줄어든 것으로 큰 속도향상이 일어나기엔 무리가 있지만, a,b값이 커질 수록 그 속도향상의 정도는 커진다.
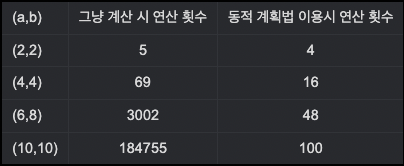
다음과 같은 경우로 DP를 이용함으로써 불필요한 중복연산을 하지 않게 처리함으로써 DYNAMIC한 속도향상이 일어나게 된다.
일반 피보나치 VS DP 피보나치
/*
/ 일반 피보나치, 코드로는 간단하지만 n이 늘어날 수록 시간복잡도와 공간복잡도가 지수스케일로 크게 늘어나게 되고
/ 결국 스택오버플로우가 일어날 가능성이 큰 구현 방법이다.
*/
int f(unsigned int n)
{
if(n <= 1)
return 1;
else
return f(n-1)+f(n-2);
}/*
/ 동적 계획법 Top-down방식으로 구현한 피보나치 함수
/ 계산한 결과를 memo에 저장함으로써 중복된 연산을 피할 수 있다.
/ 시간복잡도 역시 로그에서 최대 상수수준으로 줄일 수 있다.
*/
int memo[100]{}; //메모이제이션 공간. 전역 변수이므로 0으로 초기화
int fibonacci(unsigned int n)
{
if (n<=1) //0번째, 1번째 피보나치 수
return n;
if (memo[n]!=0) //메모가 있는지 확인(0으로 초기화되었으므로 0이 아니라면 메모가 쓰인 것임)
return memo[n]; //메모 리턴
memo[n]=fibonacci(n-1) + fibonacci(n-2); //작은 문제로 분할
return memo[n];
}'Computer Science > 알고리즘' 카테고리의 다른 글
| 넓이 우선 탐색(BFS), 깊이 우선 탐색(DFS) (0) | 2022.05.25 |
|---|---|
| 탐욕 알고리즘(Greedy Algorithm) (0) | 2022.05.13 |
| 병합정렬, 힙정렬(Merge sorte, Heap sort) (0) | 2022.05.06 |
| 버블정렬(bubble sort), 퀵정렬(quick sort) (0) | 2022.04.27 |
| 완전탐색(Exhaustive Search), 이분탐색(Binary Search) (0) | 2022.04.05 |